
Research that produces novel results, statistically significant results (that is, typically p < 0.05) and seemingly 'clean' results is more likely to be published 2, 3. A central cause for this important problem is that researchers must publish in order to succeed, and publishing is a highly competitive enterprise, with certain kinds of findings more likely to be published than others. R Foundation for Statistical Computing.It has been claimed and demonstrated that many (and possibly most) of the conclusions drawn from biomedical research are probably false 1. R: A language and environment for statistical computing. Data analysis using regression and multilevel/hierarchical models. pwr: Basic functions for power analysis (Version 1.3-0). Simulating data forces us to think about how we’re going to analyze our data, which in turn makes us confront our assumptions about how the data are generated. This would make our simulation and subsequent analysis more complicated, but it may be necessary to get accurate estimates of power and sample size. If we wanted, we could build in more assumptions, such as unequal variances between groups, unequal sample sizes per group, block effects to account for different people throwing the airplanes, and so forth. It simply gives us an approximate sample size to aim for given what we believe might be true about our paper airplane designs. It doesn’t guarantee we’ll find large effects and get “significant” results.
It appears we need about 15 times the sample size (150 per group versus 10 per group) to detect the hypothesized interaction with decent power! (See this blog post for more insight on sample sizes for interactions.)Īgain, this is all one big thought experiment based on our assumptions. To begin, let’s just simulate one data set and one analysis. What power do we have to detect a difference of 12 inches for design “b” with a significance level of 0.01, assuming a sample size of 10 per group and a common standard deviation of 10 inches between the four groups? That’s 2 x 2 = 4 combinations of paper airplanes. Perhaps we have two designs (a and b) and two weights of paper (20 lb and 28 lb).

Let’s say we want to investigate the effects of different weights of paper and different designs of paper airplanes on the distance flown in inches. But simulation can be very helpful when your experiment is more complicated. If you run this code, you’ll get slightly different answers because we’re using simulated data.įor a simple experiment such as coin flipping, simulation isn’t necessary to determine power and sample size. It looks like we would want to do around 100 flips for about 90% power, which agrees with our previous result using the pwr.p.test() function. We also specify our sample size, our significance level, and the direction of our alternative hypothesis. We use the ES.h() function to calculate effect size of 0.65 versus 0.50. In R we can use the pwr.p.test() function in the pwr package. In simple experiments such as this, it is relatively easy to calculate power. Ideally we want power to be high, say, greater than 0.90. Assuming our hunch is correct, that the coin lands heads 65% of the time, what is the probability of correctly rejecting the null hypothesis? That’s power.

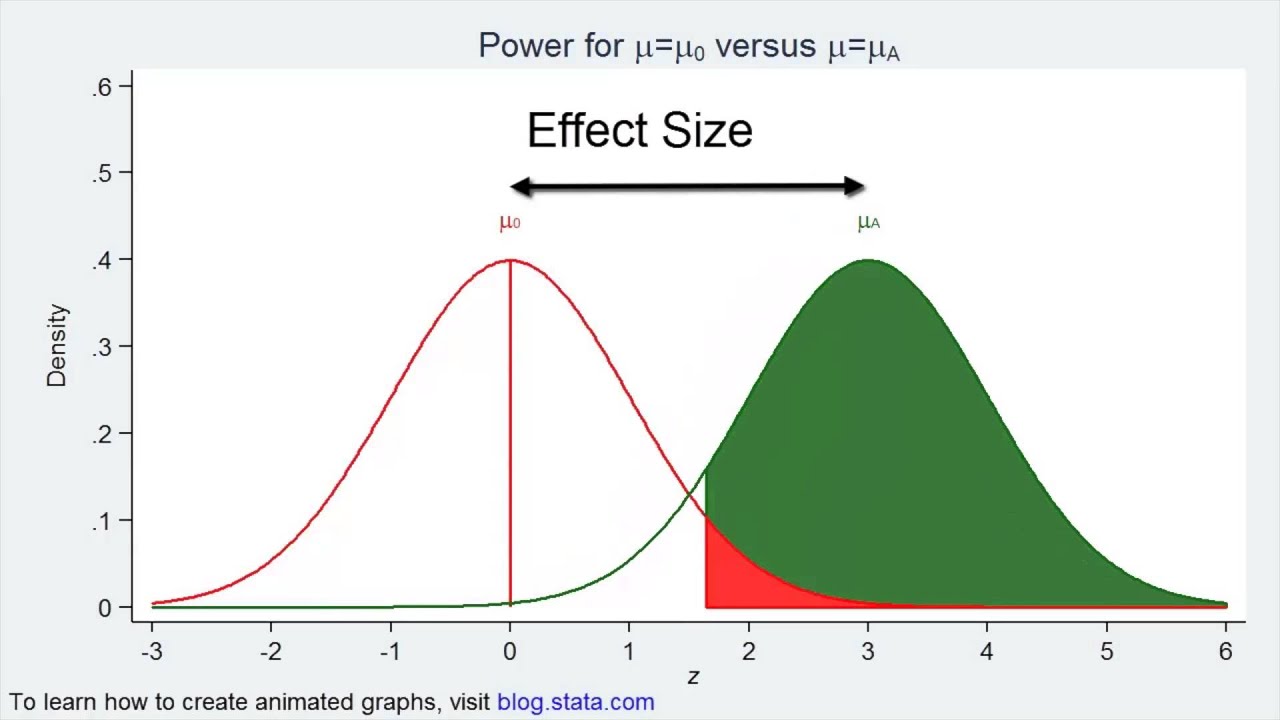
We’ll reject the null hypothesis if our p-value is below 0.05. We’ll analyze the data using a one-sample proportion test. We plan to flip the coin 50 times and calculate the proportion of heads. The alternative hypothesis is the coin is biased to land heads.The null hypothesis is the coin is not biased to land heads.For example, let’s say we suspect a coin is not fair and lands heads 65% of the time. The power of a test is the probability of correctly rejecting a null hypothesis.


 0 kommentar(er)
0 kommentar(er)
